机器学习到word2vec
最近发现,NLP(自然语言处理)很适合机器学习入门,适用场景丰富,功能强大,蕴藏着丰富的数学知识;又不至于让人陷入过多的细节,进而怀疑人生。最早看fastText,意外的清晰易懂;随后踏进交叉熵和SVM的泥沼,差点淹死。入门选择格外重要,PRML太墨迹了,陷进数学细节说的就是这本书;上来就看LDA,可能会疯。
word2vec作为优秀的词向量生成工具,自带精炼源码,背后的思想也具备很强的通用性。希望能借这篇文章,详述几个问题:机器学习是什么以及如何解决实际问题、词向量的价值、word2vec的原理,最好还能把损失函数、LR、神经网络和降纬这几个常见概念说清楚;内容皆以我的理解为基础,不一定标准且精确(尽量不跑偏),算一篇入门小总结。
机器学习
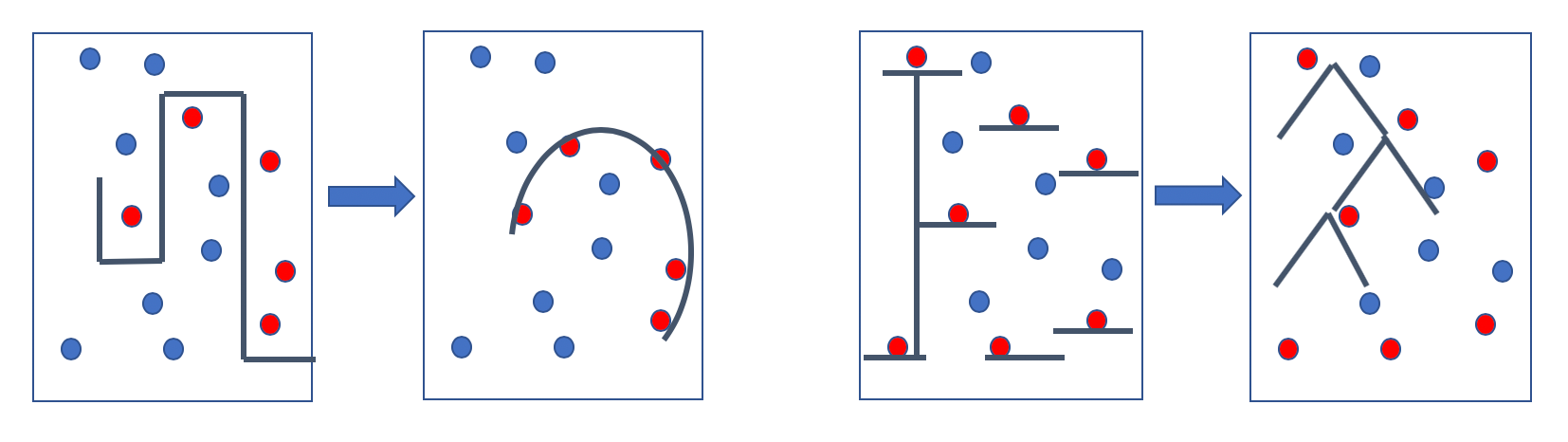
机器学习旨在利用大量样本,构造出一套人很难想出、想全甚至理解的规则系统,用这套规则来处理新的样本,产生令人满意的结果。对于简单的场景,几百个if-else能很好的解决问题,如上图所示,要区分红蓝点,人可以判断,类似画一条一条的线,把红蓝隔离开;当场景变复杂,所需的线会更细小、更繁复,维护成本很高,需要耗费大量精力去理解某条规则从何而来。举个例子,要判断一次远程登录是否异常,需要登陆时间、ip、执行的命令、查看的文件等特征,手写的话可能是:
...
if ((A && B && C) || (!C && D && E) && (F && G)) then
return Evil
else if ((A && B && !C) || (C && G && H) && (K && X)) then
return Evil
...
新增条件要很谨慎,且越往后越没人能说清楚各种缘由;这依然算简单场景,在推荐这个常见场景下,人为定规则是天方夜谭。退一步,“猫”和“狗”是否相似我们都很难用规则描述,对于喜欢萌宠的人来说,可能差不多;如果是猫奴,给他推荐狗,岂不荒唐。一篇讲旅游的文章,推荐相机镜头、酒店住宿都是很符合逻辑的,但是没办法依赖人工规则去识别文章主题(NLP真是很典型的机器学习应用场景),更没办法扩展推荐。
上图从左到右就是规则到模型的进化,机器学习发展到现在,通用模型基本能覆盖到我们的数据特征:或者是类似函数的一条曲线、或者是类似多叉树的一层一层判断(其实就是机器版if-else)、或者更复杂的模型。有了通用模型,我们不必关注规则本身,可以把精力放在如何提高效果,繁杂工作交给模型。
抽象成数学问题,有大量的样本,包含多个特征,以及已知的结果——标注或者通过其它手段得到(这里先忽略非监督学习等);根据经验选择适合的模型,如线性模型或树模型,把样本交给他,训练出一套规则系统——对于线性模型,每个特征对应一个参数,代入公式,算出结果;对于树模型,则更复杂一些,根据每个特征的取值逐层划分。新的未知结果的样本,只要有特征值,就可以算出结果:是否是黑客攻击、是否可以关联推荐、文章主题等。
$$Sample = (x^1_1,x^1_2,x^1_3,…,x^1_n, y^1) \ \text{->} \ f(x^i) = y^i \ \text{->} \ f(x^m)$$
有人可能会问,这个靠谱嘛?能完全准确吗?答案显然是不能,模型不可能像人工规则一样准确无误,甚至不可解释。但是正如此前所说,很多问题没办法列出规则,模型能处理80%甚至95%的情况,已经很优秀了,总比0%要强。
简单来说,模型能够从大量样本中学到人很难发现的规律,并将学习结果泛化到新的样本,泛化能力是评价模型好坏的重要参考之一。
机器学习是一门很复杂的学科,背后是严谨的数学在支撑,这里只为方便理解;但是即便非监督学习、深度学习和强化学习,思路和用处是类似的。
现在大家越来越清楚何时该依赖模型,规则的作用也会被逐步重视,没有一招鲜万金油,都要具体业务具体分析。
损失函数
那么模型究竟是如何工作的呢?样本交给模型,和得出正确参数和规则系统之间,是用损失函数连接的。损失函数衡量模型误差,上面提到的模型最终参数或者树何时分叉很难一步到位,因此需要大量数据,计算出误差,再通过修改参数,让误差收敛,反复迭代,得出较满意的结果(训练方法随模型而不同,这里同样只是科普某个特例)。
以简单的线性模型为例,解释损失函数的作用以及模型如何迭代收敛。
$$假设函数:y_p=p_0 + p_1x_1 + p_2x_2 + … + p_n*x_n = \sum_0^np_ix_i;\ \ x_0=1;$$
$$损失函数:J(p) = \frac{1}{2}\sum_1^m(y_p^i - y^i)^2; \ \ y_p^i是预测值,y^i是实际值$$
训练模型的过程,就是损失函数减小的过程,J是关于参数p的函数;把损失函数换成矩阵表达形式,其实相当于做一次矩阵映射。简单的微积分知识可知,沿着偏导方向调整参数,可以让函数值减少。
$$p_j=p_j - \alpha\frac{\partial}{\partial p}J(p); \ \ \alpha是学习速度$$
$$\frac{\partial}{\partial{p_j}}J(p) = (y_p - y) * \frac{\partial}{\partial p_j}(\sum_0^n p_ix_i - y) = (y_p - y)*x_j$$
这就是常说的梯度下降,再次提醒,这个函数是关于p——即模型参数的函数,沿着偏导方向,可以逐步接近函数最低点,使得损失函数最小。
损失函数可以有很多种形式,平方和很常见,从极大似然概率的角度看,也能推导出最小二乘,可谓源远流长。
这里没有提及风险损失和正则化、随机梯度下降和牛顿法等基础概念。
模型评估也有一套成熟的体系,并非单纯减小损失函数;样本量再多,依然不够充分,如果模型在训练集表现过好,很可能过拟合,遇到新的样本手足无措,表现极差;正则项就是为了防止过拟合。也是为了提高模型泛化能力。
逻辑回归
常言道,“面试DNN,入职LR+规则”,这里的LR就是逻辑回归模型;人们经常把机器学习问题分为分类和回归——前者将样本分成具体类别,做离散预估;后者给样本打一个分数,预测连续值。LR是典型的分类模型,根据样本特征计算出一个分数,高于阈值标记为1,低于标记为0。
基础是sigmoid函数(s形函数),或者叫logistic函数(一种特殊的sigmoid函数):
$$g(z) = \frac{1}{1+e^{-z}}$$
$$g'(z) = \frac{d}{dz}\frac{1}{1+e^{-z}} = \frac{1}{(1+e^{-z})^2}(e^{-z}) = \frac{1}{(1+e^{-z})}*(1-\frac{1}{(1+e^{-z})}) = g(z)(1-g(z))$$
函数图像如下,可以看到值域被限定在0-1之间:
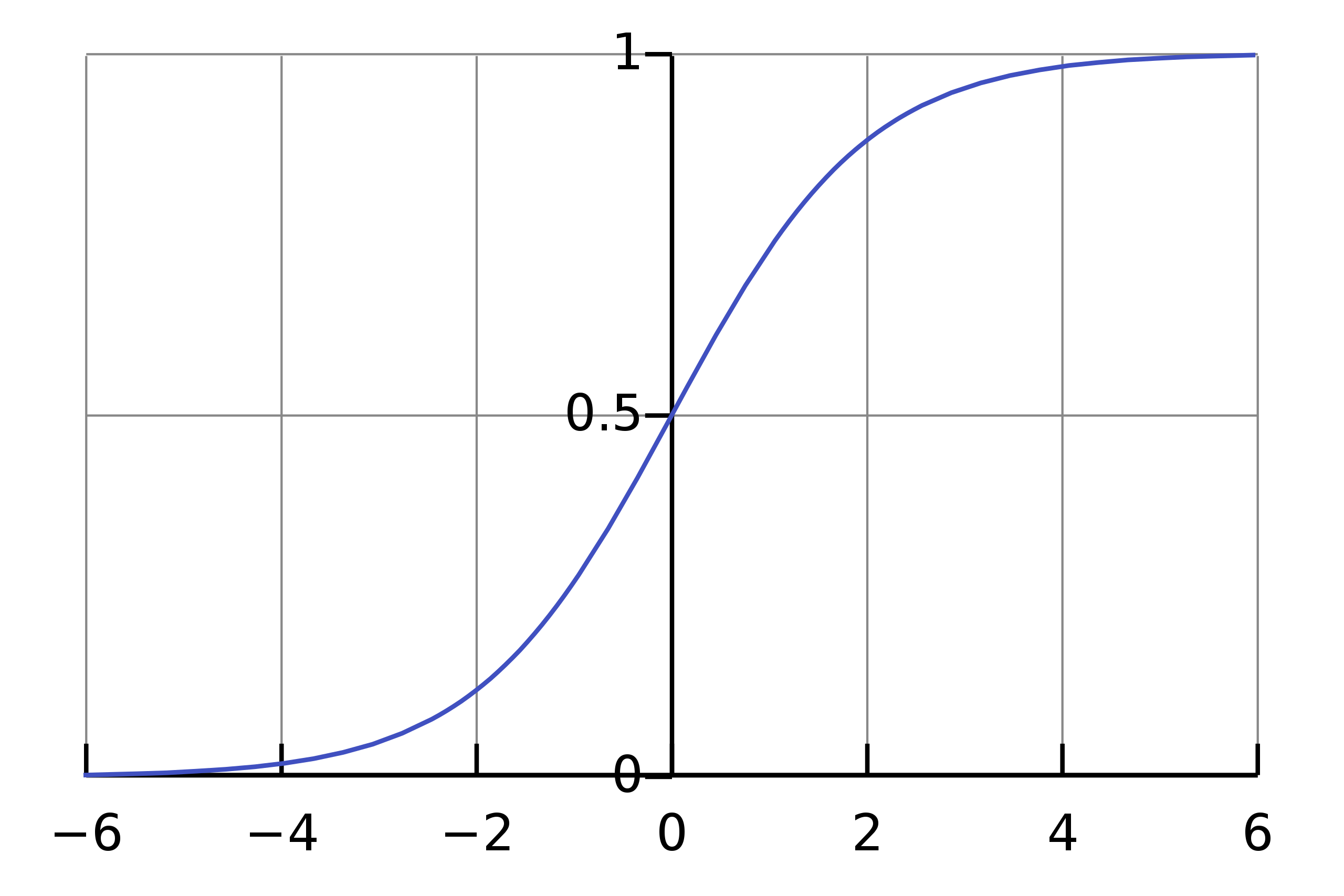
因为逻辑回归处理分类问题,采用上述的逻辑函数,平方损失函数非凸,没法通过梯度下降得到全局最优解。因此逻辑回归损失函数如下(有的h省去下标\theta,因为渲染器有点问题(囧)):
$$假设函数:h_\theta(x) = g(\theta^Tx) = \frac{1}{1+e^{-\theta^Tx}};\ \theta^T x = \sum_0^n\theta_ix_i \ \ 这里的\theta 就是上面的 p, 代表参数$$
$$损失函数:L(\hat{y},y) = -(y\log(\hat{y}) + (1-y)\log(1-\hat{y})); \ \ \hat{y} = h_\theta(x)$$
这个损失函数看起来非常合理——当y,即样本实际标签是1时,预测值越大损失函数越小;实际标签为0时,预测值越小损失函数越小。但是它从何而来呢?引入交叉熵的概念,衡量两个概率分布的差异;由于样本真实概率分布不会变,意味着KL散度(概率分布差异表征)越小,猜测的概率分布接近真是概率分布。而极大似然估计就相当于最小化训练集经验分布与真是分布的差异,即最小化KL散度。
$$y=1的概率:p(y=1|x;\theta) = h_\theta(x)$$
$$y=0的概率:p(y=0|x;\theta) = 1 - h_\theta(x)$$
$$联合概率:p(y|x;\theta) = h(x)^y(1-h(x))^{1-y}$$
$$似然函数:L(\theta) = p(y|x;\theta) = \prod_1^m p(y^i|x^i;\theta) = \prod_1^m h(x^i)^{y^i}(1-h(x^i))^{1-y^i}$$
上述似然函数的log形式,就是损失函数(取负数)。具体的梯度下降过程,同样求偏导+迭代,不难计算。
逻辑回归虽然用来解决分类问题,由于分类结果是一个概率值,也会经常用在如CTR(点击率)预估等场景
词向量
人们通常会觉得算法工程师只是在已有模型基础上做些微调,所谓“调包侠”和"调参狗";其实这两个算是高阶工种,已经可以lead项目的。新手一般只能做些特征完善之类的工作,能有幸加个新特征,都够晋升的了(更惨的可能得看一年效果,低阶“指标奴”)。以上是玩笑话,处理特征真的非常重要;最初我以为只要把特征扔进模型就可以,实际效果很差。特征会跟某个参数发生运算,最后产生结果,假设有个特征是年收入,2亿、1亿和50w,很明显前两者更接近,不能直接把数字扔进去。
回到文本处理,经常需要把某个或某些词作为特征,例如购买的商品、文章的主题词、地理位置描述等;首先想到不能分配自然数1-n给词库的n个单词,假设“火车站”和“空气”挨着,用数字78、79代表,模型想学出他们的差异太难了。一种粗暴的解法是按位分配,词库里n个词,构建一个n维向量,每个词只有一位是1,其他位是0,参数训练互不影响;即one-hot。
但是one-hot表示有很多缺点,维度太高,模型训练速度变慢;而且词之间毫无关系,“花生”和“花生米”的相似度应该极高。词向量是词的分布式表示,用一个低纬度向量表示,例如50或100维,并且词义相近的词会有较近的cos距离。
word2vec就是训练词向量的工具,本身没有太多新观点,只是很好用的tool。
神经网络
其实简单的神经网络和我们大脑神经元毫无关系,非有资料说起源于脑信号,那就姑且这么自我安慰吧。我觉得起源于线性模型没办法解决异或xor,没办法学出非线性关系,由此促进多层变换的发展,也就是神经网络。下面的这个图结构很清晰:
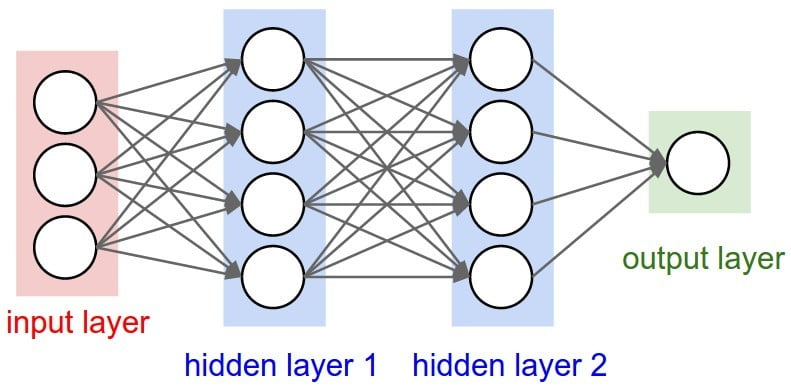
n个特征进入输入层,加上bias偏移,经过k1个sigmoid(或者其它非线性激活函数)变换,进入下一层,即第一个隐藏层;这里需要(n+1)*k1个参数。随后又是k2个sigmoid变换,进入第二个隐藏层,需要(k1+1)*k2个参数。最后又是sigmoid变换,得到输出值;这里的输出层只有一个节点,如果是多分类,会有多个output。这个过程就是正向传播,跟LR没有什么本质不同。
正向传播计算出结果,需要用正确结果来修正,这里用的损失函数与LR的损失函数一样,都是交叉熵和极大似然推导出来的(可能会有多分类)。在输出层计算出预测值与实际值的误差,逐层向上,计算出每层需要做出的修正,类似梯度下降;这个过程称为反向传播。下面对一个样本做一次正向传播和反向传播。
$$正向传播:a^1 = x^1, a^2 = g(\theta^1a^1), a^3=g(\theta^2a^2), \hat{y}=g(\theta^3a^3)$$
$$反向传播:\delta = \hat{y}-y, \delta^3=(\theta^3)^T\delta.*g'(\theta^2a^2), \delta^2=(\theta^2)^T\delta^3.*g'(\theta^1a^1)$$
对每个样本正向传播+反向传播计算出每层的参数误差,然后修正。本质上是将误差也按照正向传播时节点权重向前分配,利用链式求导法则,折算出梯度,反向传播将这一过程简化。
神经网络输入和输出之间的隐藏层,可以看作对数据做的中间层加密,经过一次变换输出结果;比起原始输入,隐层结果更能表征样本间关系。
word2vec
word2vec接收预料库,给每个词分配长度为m的词向量(存在hash字典里),每轮训练都会修改词向量,最终迭代完成,得到结果。有两种模型:基于当前词预测上下文和基于上下文预测当前词,最终目标都是求条件概率最大。
- CBOW(Continuous Bag-of-Words Model): 输入前后k个词都词向量,隐藏层对向量求和,输出是各个词向量的概率,根据是否是当前词做修正。
- Skip-gram(Continuous Skip-gram Model): 输入当前词向量,隐藏层忽略不计,输出还是各个词向量概率,根据是否位于上下文做修正。
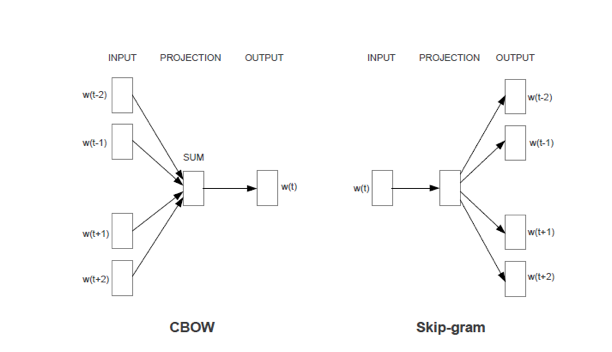
输出应该是所有的词向量的概率,总共n个;但是这样输出层太多,而且干扰也很大,毕竟绝大多数都不在上下文。word2vec有两种处理方法:huffman树或负采样。huffman树根据词频将词编码,这样输出会变成长度为logN,从根节点到叶子结点的路径;左节点是1,右节点是0,然后做极大似然,训练logN个参数。负采样更简单,对不在上下文对词根据词频等做加权采样,得到L个输出结果,然后就是普通的神经网络训练。
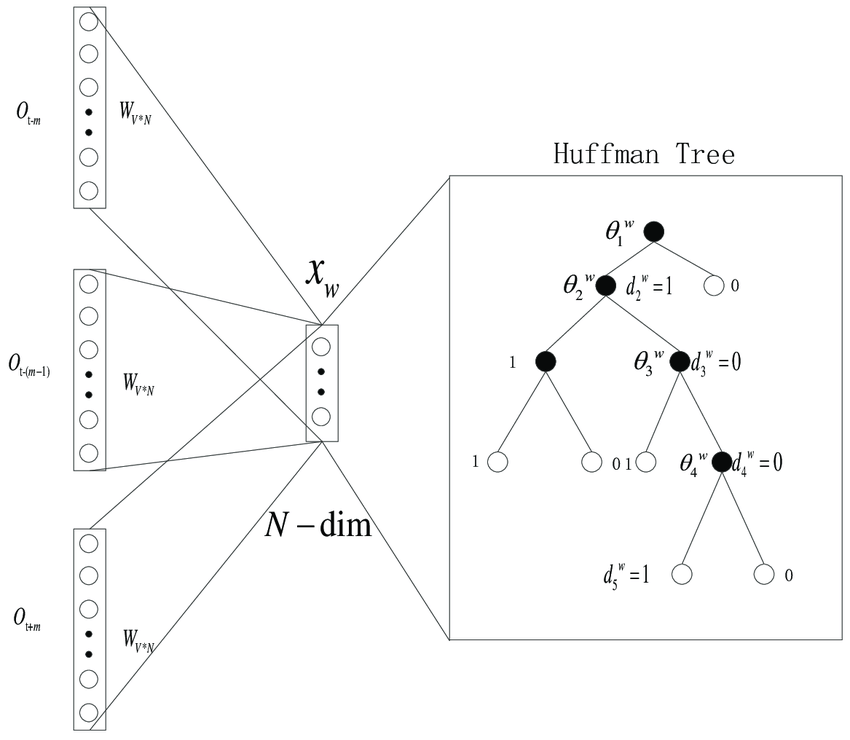
数学运算不复杂:
$$左节点和右节点概率: \ P(+) = \sigma(x_w^T\theta) = \frac{1}{1+e^{-x_w^T\theta}} ,\ P(-)=1-P(+)$$
$$单个词的似然函数: \ \prod_1^kP(n_i, i) = \prod_1^k(P(-)|P(+)),k=depth(Huffman)$$
$$目标函数: \ L = log\prod_2^l P(d_j^w|x_w,\theta_j^w) = \sum_2^l[(1-d_j^w)log[\sigma(x_w^T\theta)] + d_j^wlog[1-\sigma(x_w^T\theta)]$$
最后用梯度上升求解极大似然。
站在现在看,会觉得word2vec是很自然的想法,但是任何事情都是一步一步发展而来的,并非平地起高楼。这其实也提醒我们,一定要站在行业前沿,不然折腾半天都是别人几年前就玩剩下的。
GloVe也是很常用的词向量生成工具,不同于word2vec基于概率,前者基于count——共现概率比值。
SVD等矩阵分解方法,也经常用于生成词向量。
总结
意外发现,《基于深度学习的自然语言处理》组织结构和这个小破文很一致,看起来有深度有广度,等我看完可以再修正这篇总结。